inspirit
Geheimnisse guten Designs
DER GOLDENE SCHNITT · Phi Φ · die Fibonacci-Reihe
erfüllen eine geheime, doch ganz offensichtliche Mission. Diese universellen Ordnungsprinzipien sind generell in organisch Gewachsenenem, also auch in uns Menschen, formgebend und genial funktional. Nach ihnen sind die Proportionen des menschlichen Körpers, des Gesichtes, der einzelnen Glieder wie Arme, Beine, Hände bis in den kleinen Finger, ja auch die der inneren Organe, eingeteilt. Ebenso sind die Proportionen der Körper von Tieren und Pflanzen perfekt in den goldenen Maßen aufeinander abgestimmt. Natürliche Landschaften formen sich fraktal. Somit ist dies ein offenes Geheimnis für gutes Webdesign, Grafikdesign bzw. jegliches Design. Denn der Mensch neigt sich instinktiv eher Ähnlichem und Vollkommenem zu.
Goldener Schnitt
goldene Proportionen
Die Harmonie, die diese divine Ratio erzeugt, wirkt sofort wohltuend auf unser Unterbewusstsein und unseren natürlichen Hang zu qualitativer Schönheit. Phi Φ und die sogenannte Fibonacci-Reihe zeigen sich in den verschiedensten Bereichen als eine Art Maß und Algorithmus der Matrix, der schöpferische Logos des selbstregulierenden Chaos. Ob in der Biologie bzw. Natur, Mathematik, Geometrie, Astronomie, Quantenphysik, klassischer Physik, in Kunst und Design, in der Theologie bzw. den heiligen Büchern, neuerdings in der Informatik, der Marktentwicklung und - eben deutlich sichtbar auch bei Proportionen des Menschen, Tieren und Pflanzen. Diese »Divina Proportione« lässt als Grundlage der perfekten Harmonie automatisch Resonazphänomene entstehen. Phänomenal ist zudem, dass es dabei nicht nur um die Schönheit, sondern um die optimalen Funktionsabläufe und Synchronizitäten geht, die durch diese Proportionen in fraktalen Abläufen bzw. Entwicklungen gewährleistet werden. Φ=1,6180339...
»divine Ratio«
Große »eingeweihte« Geister, wie Leonardo da Vinci, erkannten dies und wendeten es in ihren Werken stets an. Das von ihm angeregte und illustrierte, 1905 in Venedig erschienene Buch, »De divina proportione« (Die heiligen Proportionen) seines Mathematiklehrers Luca Pacioli, befasst sich ausgiebig mit diesem hoch interessanten Thema. Es gibt inzwischen sehr viel Literatur online und auf Papier zum Goldenen Schnitt. Meist wird es hierzulande der »Goldene Schnitt«, das »Goldene Maß«, die »Goldene Zahl«, die »Göttliche Proportion«, anderslandig auch »Divine Ratio«, the »Golden Ratio«, the »Golden Number« und auch »Divine Proportion« ... genannt.
Phi Φ, die sogenannte Fibonacci-Reihe & eine geheime Mission
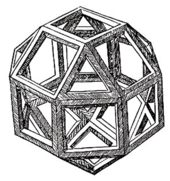
Große "eingeweihte" Geister, wie Leonardo da Vinci, erkannten dies und wendeten es in ihren Werken stets an. Das von ihm angeregte und illustrierte, 1905 in Venedig erschienene Buch, «De divina proportione» (Die heiligen Proportionen) seines Mathematiklehrers Luca Pacioli, befasst sich ausgiebig mit diesem hoch interessanten Thema.
Es gibt inzwischen sehr viel Literatur online und auf Papier zum Goldenen Schnitt. Meist wird es hierzulande der »Goldene Schnitt«, das »Goldene Maß«, die »Goldene Zahl«, die »Göttliche Proportion«, anderslandig auch »Divine Ratio«, the »Golden Ratio«, the »Golden Number« und auch »Divine Proportion« ... genannt.
Interessant, doch weniger bekannt ist die Bezeichnung des Orthogons (des Goldenen Rechtecks) als »Golden Auron«. Es ist nicht gänzlich erwiesen, woher die Bezeichnung stammt. Im Lateinischen bedeutet »Aureus« vergoldet oder auch edel, im Keltischen gibt es den Namen: »Ayr-on«, der sich aus »aur« (Gold) und »on« (ein göttliches Ende oder Tod) zusammensetzt. (Quelle: urbandictionary.com, goldennumber.net/orthogons/)
Dabei handelt es sich um die auf der Startseite und hier rechts gezeigte Konstruktion bzw. eine der geometrischen Möglichkeiten zur Erzeugung des Goldenen Schnittes Φ und des goldenen Rechteckes, wenn man noch einen Schnittpunkt oben links, adäquat zum rechten, hinzufügt.
Φ erzeugt harmonisches Design in Resonanz zum Menschen. Oder Φ und Sie
Es ist ein besonders schönes Beispiel, wie die menschlichen Proportionen und eine perfekte Komposition, die auch im gesamten Bild mit dem goldenen Schnitt korrespondieren, bewusst ein Gefühl der Harmonie und Perfektion göttlicher Schöpfung erzeugen. Dies konnte man schon in dem Gemälde der Mona Lisa bzw. Gioconda, bewundern, sowie auch in allen anderen Werken Leonardos. Er soll ein absoluter Perfektionist gewesen sein.
Seine analytischen Untersuchungen der menschlichen Proportionen vom Säugling bis zum Alten sind in einigen seiner Zeichnungen zu sehen und zeigen die Gewissenhaftigkeit, die in seine Genialität einfloss. Sie beweisen, dass die Anwendung der »Divina proportione« bei seinen Arbeiten kein Zufall war.
Alles was mit den universellen Goldenen Maßen Phi und somit denen der Fibonacci-Reihe, welche ja miteinander korrespondieren, gestaltet ist, wird unbewusst als harmonisch und anziehend empfunden. In der Quantenphysik sagt man, es geht mitteinander in eine gewisse Resonanz bzw. Interferenz, es korrespondiert miteinander. Deshalb ist ein ganzheitliches Design unter diesen Aspekten besser als ein oberflächlich angelegtes.
Inhaltliche Quellen: Priya Hemenway, »Der geheime Code«, Evergreen GmbH, 2008 und Wikipedia
Hier sehen Sie das berühmte Bild Leonardos zu den menschlichen Proportionen, noch ergänzt mit einigen weiteren Einteilungen.
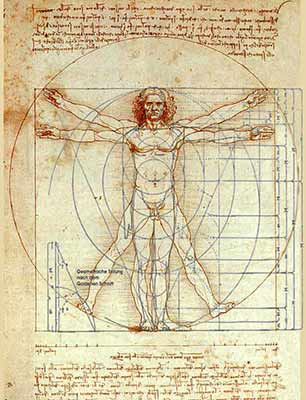(Bildquelle: WikipediaVon Leonardo da Vinci - Leonardo Da Vinci - Photo from www.lucnix.be. 2007-09-08 (photograph). Photograpy:This image is the work of Luc ViatourPlease credit it with: Luc Viatour / https://Lucnix.be in the immediate vicinity of the image. A link to my website https://lucnix.be is much appreciated but not mandatory.An email to Viatour Luc would be appreciated too.Do not copy this image illegally by ignoring the terms of the license below, as it is not in the public domain. If you would like special permission to use, license, or purchase the image please contact me Viatour Luc to negotiate terms.More free pictures in my personal gallery[Note: this is in the public domain, despite the photographer's contradictory claim. Any use is permissible, and no credit to the photographer is necessary.]Nikon case D80 optical Sigma 17-70mm F2,8/4,5 Macro, Gemeinfrei, Link) 
Die Fibonacci-Reihe als universale Spirale der Natur
Nachdem die Kaninchenfrage geklärt war, ließen weitere Anwendungen und Entdeckungen zur Fibonacci-Reihe nicht auf sich warten. Denn ganzheitlich denkende Geister wussten schon immer, dass in Gottes Schöpfung das perfekteste Design zu finden ist. Die Genealogie bei Bienen weist das gleiche Schema auf. Das Wachstum von Pflanzen, speziell die Anordnung der Blätter, Äste und Zweige um den Stamm herum, geschieht fast ausschließlich im Fibonacci-Logarithmus bzw. der Fibonacci-Spirale.Das geniale dabei ist, das diese Anordnung nicht nur schön aussieht, sondern auch gewährleistet, dass so viel Sonnenlicht wie möglich an jedes Pflanzenteil gelangen kann.
Die Blüte einer Rose ist ein schönes Beispiel für die Anordnung der Blütenblätter im Fibonacci-Algorithmus, genau im »Goldenen Winkel« (137,5 Grad) und in der Fibonacci-Spirale.
Die Hörschnecke im menschlichen Ohr windet sich in einer Fibonacci-Spirale, ebenso wie teilweise die äußere Ohrmuschel und jedes Haarfollikel.
Geometrisch kann die Spirale u. a. entwickelt werden, wenn (der Fibonacci-Zahlenreihe entsprechend) aus anfangs 2 kongruenten Quadraten immer ein weiteres Quadrat mit der Gesamtseitenlänge der vorhergehenden beiden Quadrate hinzukommt. Dadurch entstehen wieder Goldenene Rechtecke bzw. Annäherungen daran.
Bildquelle Rose: Pixabay LoboStudioHamburg/ Inhaltliche Quellen: Priya Hemenway, »Der geheime Code«,Evergreen GmbH, 2008 und Wikipedia
Wie Fibonacci mit einigen Kaninchen die Wissenschaften revolutionierte
Der heute als Fibonacci bekannte Namensvetter Leonardo da Vincis, war der in Pisa geborene Sohn eines Diplomaten namens Leonardo von Pisa. Allerdings wuchs er in Bugia, heute Bejaïa, einer Hafenstadt in Algerien auf, wo er auch unterrichtet wurde. Zu dieser Zeit blühten Wissenschaften, Kunst und Handel im Gegensatz zu Europa dort schwunghaft und inspirierten den auf Wunsch des Vaters angehenden Buchhalter.»Als ich dort die indische Kunst der neun Symbole kennenlernte, eine bemerkenswerte Lehre, gefiel mir sehr bald dieses Wissen um die Kunst über alles und ich studierte mit ihnen, wer auch immer darin gelehrt war, vom nahen Ägypten, Syrien, Griechenland, Sizilien und der Provence und praktizierte deren verschiedene Methoden.«
(Mit Kunst meinte er die Kunst der Mathematik, die seinerzeit tatsächlich noch als solche angesehen war, hierbei speziell die neun eigentlich arabischen Zahlen, welche die römischen Ziffern später ablösten) Fibonacci in »Liber abacci« Da er den Nutzen all dessen für alltägliche praktische Anwendungen erkannte, entwickelte er bezüglich einer solchen die berühmte Fibonacci-Reihe.
Er wurde beuftragt, die Anzahl an Kaninchen zu ermitteln, die während eines Jahres in einem abgetrennten Terrain entstünden. Dabei sollte davon ausgegangen werden, dass jedes vorhandene und jedes neue Kaninchenpärchen ein weiteres Pärchen Junge bekommt.
Die Reihe an sich war ihm von den arabischen und indischen gelehrten Schriften bzw. Lehrern als die "neuen indischen/arabischen Symbole" bekannt - wobei es sich um die Zahlen 0 bis 9 handelte. Sein Verdienst und seine Genialität war, dass er dies um einige eigene Anwendungsentwicklungen bereicherte sowie hohe Mathematik damit betrieb, die seiner Zeit weit voraus war, und dies nach Europa brachte. Er schrieb sein im Jahre 1202 in Pisa herausgegebenes Buch »Liber abacci« so verständlich, dass nicht nur die Elite, sondern auch ein einfacher Händler mit diesen Berechnungen arbeiten konnte. Das ließ diese Mathematik sehr schnell populär werden, außerdem war sie viel praktischer als das bis dahin verwendete System mit römischen Ziffern.
Die Kaninchenfrage löste er mit der Reihe folgendermaßen: Man geht davon aus, dass ein Kaninchen einen Monat reift, bevor es Junge bekommt. Das erste einen Monat alte Pärchen bekommt im 2. Monat ein Pärchen Junge. Diese reifen einen Monat, währenddessen die Eltern ein weiteres Pärchen Junge bekommen. Jetzt sind es also drei Kaninchen-Pärchen insgesamt im 3. Monat. Während des 4. Monats bekommt das erste Elternpaar wieder Junge, ihr erstgeborenes Jungenpärchen bekommt ebenfalls ein Pärchen Junge. Also gibt es im 4.Monat insgesamt 5 Pärchen. So setzt bzw. pflanzt sich das weiter fort.
Das Interessante dabei ist, das jede Zahl der Reihe die Summe der beiden vorhergehenden ist und das Verhältnis zweier aufeinanderfolgender Zahlen sich mit steigender Reihe immer exakter dem goldenen Verhätnis Phi von 1,6180339 annähert. So ist z. B. an 22. Stelle 10946/6765=1,61803399852...
Rechts sind die ersten Zahlen der unendlichen Fibonacci-Reihe zu sehen. 0
1
1
2
3
5
8
13
21
34
55
89
144
233
377
610
987
1597
2584
4181
6765
10946
17711
...
Die Kaninchenfrage löste er mit der Reihe folgendermaßen: Man geht davon aus, dass ein Kaninchen einen Monat reift, bevor es Junge bekommt. Das erste einen Monat alte Pärchen bekommt im 2. Monat ein Pärchen Junge. Diese reifen einen Monat, währenddessen die Eltern ein weiteres Pärchen Junge bekommen. Jetzt sind es also drei Kaninchen-Pärchen insgesamt im 3. Monat. Während des 4. Monats bekommt das erste Elternpaar wieder Junge, ihr erstgeborenes Jungenpärchen bekommt ebenfalls ein Pärchen Junge. Also gibt es im 4.Monat insgesamt 5 Pärchen. So setzt bzw. pflanzt sich das weiter fort.
Das Interessante dabei ist, das jede Zahl der Reihe die Summe der beiden vorhergehenden ist und das Verhältnis zweier aufeinanderfolgender Zahlen sich mit steigender Reihe immer exakter dem goldenen Verhätnis Phi von 1,6180339 annähert. So ist z. B. an 22. Stelle 10946/6765=1,61803399852...
Rechts sind die ersten Zahlen der unendlichen Fibonacci-Reihe zu sehen. 0
1
1
2
3
5
8
13
21
34
55
89
144
233
377
610
987
1597
2584
4181
6765
10946
17711
...
Bildquelle Kaninchen: Pixabay/ Inhaltliche Quellen: Priya Hemenway, »Der geheime Code«,Evergreen GmbH, 2008 und Wikipedia
»Golden Auron«
Das Ganze verhält sich zum Größeren wie das Größere zum Kleineren.b/a=φ=1.6180339
61,8034%+38,1956%=100% Harmonie
Halbiert man ein Quadrat, zeichnet ein Kreissegment um den Schnittpunkt der Teilungslinie mit der Quadratumfangslinie mit dem Radius der Diagonalen, erhält man im Schnittpunkt der Kreisumfangslinie und der Verlängerung der Quadratlinie a (mit dem Kreismittelpunkt) das Maß b, das sich zu a genau im goldenen Schnitt verhält. Dies ist Φ = 1,6180339
»Goldener Schnitt in der Architektur«
Dass die Bauten schon in der Antike nach dem Goldenen Schnitt gebaut wurden, vor allem die sakralen Bauten, ist bekannt. Das Parthenon der Akropolis ist eines der prominetesten antiken Beispiele.Die Kathedrale von Chartres, bis heute geheimnisumwittert, ist ein genialer sakraler Beweis für das hohe Maß an Hintergrundwissen um den Goldenen Schnitt des bis heute angeblich unbekannten Baumeisters. Ihr Grundriss beruht u. a. auf einem Pentagramm und somit auf den Goldenen Proportionen. Er wird bis heute als Geheimtipp für eine besondere Meditation zur Erreichung höherer Bewusstseinzustände verwendet, die u. a. von bestimmten Zigeunern überliefert wurde.
Der große griechische Bildhauer und Architekt Phidias (auch Pheidias 500-432 v. Chr.) soll als Erster bewusst den Goldenen Schnitt in seinen Werken angewendet haben. Von ihm ist auch der Name Phi bzw. das Zeichen Φ abgeleitet worden.
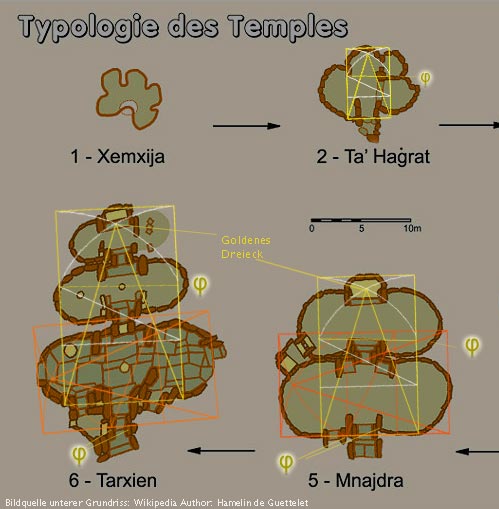
Meine Untersuchung der Proportionen der Spiralornamente einer den Eingang bewachenden Steinplatte und eines Altars im Tarxien-Tempel, sowie einiger Grundrisse der uralten Tempel auf Malta ergibt, dass auch dort der Goldene Schnitt nicht unbekannt gewesen sein dürfte. Zufall? Diese mysteriösen Bauwerke gelten heute, nach denen in Göbelki Tepe (Türkei), als die ältesten noch vorhandenen Steinbauten der Menschheit. Wenn man sich die Entwicklung der Grundrisse ansieht, mutet sowohl die organische Form, als auch die Veränderung derer (3. Abb. Zeitl. Ablauf v. oben links-unten links) wie eine Illustration bestimmter Entwicklungs-/Einweihungsstufen an. Zudem wurden sie nach bestimmten kosmischen Konstellationen, unter Berücksichtigung der Präzession, ausgerichtet.
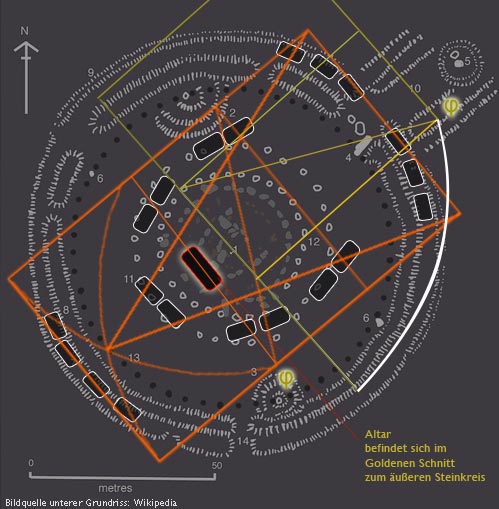
Auch der Grundriss vom jüngeren, aber berühmteren Stonehenge (4. Abb.) weist den goldenen Schnitt auf.
Untere Grundrisse:
By Hamelin de Guettelet (travail personnel d'après Trump) [Public domain], via Wikimedia Commons Par Hamelin de Guettelet — travail personnel d'après Trump, Domaine public, Lien/ Quelle Wikipedia (Typologie des Temples,) Malta, v. Hamelin de Guettelet
CC BY-SA 3.0, Link: Quelle Wikipedia Grundriss Stonehenge
Sie sind an ganzheitlich durchdachten und individuellem Design interessiert?
Sehen Sie hier → Kundenreferenzen mit Wordpress-Webseiten und Informationen
Mehr Informationen und einige Kundenreferenzen mit statischen, noch → nachhaltigeren Webseiten sehen Sie hier. Auch die eigene Seite ist eine solche.
Wenn Sie zügig zu einem neuen oder überarbeiteten Web-oder Grafikdesign kommen wollen, können Sie gern hier ein → schnelles Briefing bzw. Anfrage starten.